关于排名的excel公式有:RANK函数、COUNTIF函数、中国式排名SUMPRODUCT函数、倒数排名RANK函数。其中rank函数的排名方式只有两种,一个是0值的升序排名,另一个则是非0值的降序排名。
又到了今天的学习时间,作者来分享关于排名的几个函数公式,不管是常规排名,还是非常中国式的排名,或者是倒数排名,只要学会以下几个公式,都能轻松搞定所有排名问题。
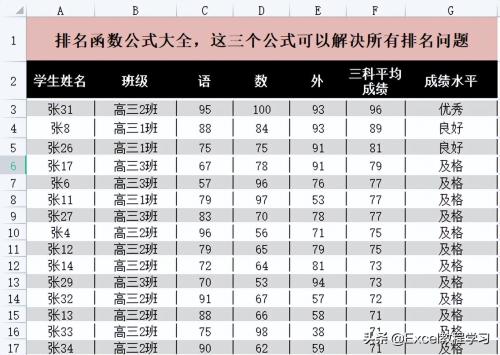
直入正题,我们需要对下图中学生的”三科平均成绩“进行排名,成绩从高至低一次排名。
所谓的常规普通排名,即有相同排名时会跳过之后的排名,例如5,4,4,3四位数,普通排名为1,2,2,4;
而中国式排名,有相同排名时不会跳过后续的排名,如5,4,4,3四位数,中国式排名为1,2,2,3.
公式一:RANK函数
首先介绍在excel中计算排名的专用函数——rank。
rank函数的表达式为:=rank(数值,引用区域,排位方式)
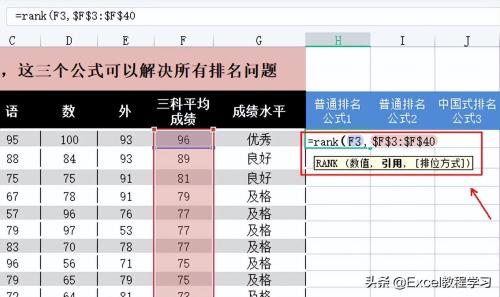
RANK函数三个参数中,最后一个参数可以省略,默认为0,即升序排序。
按照它的表达式,可以输入公式:=RANK(F3,$F$3:$F$40)
便得到了学生们三科平均成绩的排名。
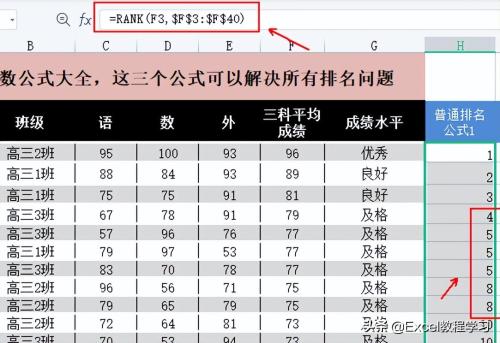
公式二:COUNTIF函数
countif函数实际是计数函数,用来统计一个区域中符合指定条件的单元格个数。
它的表达式为:=countif(区域,条件)。
看上去语法非常简单,就两个参数,而第1参数区域通常是固定的,重点在于条件的设置。
在表格中,我们要计算平均成绩排名,条件可以设置为大于学生的三科平均成绩,即>f3,作者先写下完整公式,再通过一个例子来详细说明它的含义。
公式为:=COUNTIF($F$3:$F$40,">"&F3)+1
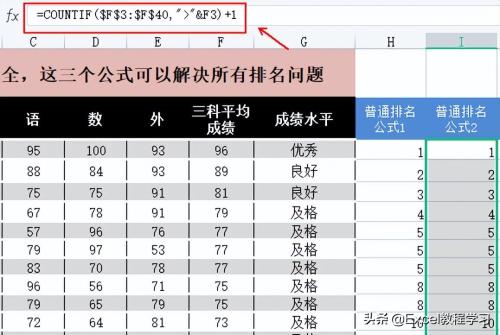
这个公式的含义是在计算$F$3:$F$40单元格区域中,数值大于F3数值的单元格个数。这里要注意单元格的引用方式,区域为绝对引用,条件是相对引用,这样才能正确填充公式。
如公式所写,F3的值是96,当条件">96"时,我们的计数区域中并不存在大于96的数值,因此countif函数公式的结果为0,于是再加上1,便得到了排名结果。
当条件为">F4",值为89,而$F$3:$F$40单元格区域中大于89的单元格有1个,即F3,最后再加上1,结果便得到排名2;依次计算下去,可以得到所有的排名。
通过countif函数的计数作用来排名,倒是一个灵活通变得方法。
公式三:中国式排名SUMPRODUCT函数
sumproduct函数,也叫乘积函数,更完整的叫法,应该是乘积求和函数,因为它的作用就是对单元格的乘积进行求和。
这个函数在excel中的应用很广泛,尤其在之前的老版本中,官方还没有更新一些强大的新函数,比如sumifs函数,如果没有sumifs函数,那怎么快速地多条件求和呢?大家首先的自然是sumproduct函数。
关于该函数的使用大全,我们可以用一篇文章来详尽介绍,但今天先来求解排名的公式写法。
我们输入公式:=SUMPRODUCT(($F$3:$F$40>F3)*(1/COUNTIF($F$3:$F$40,$F$3:$F$40)))+1
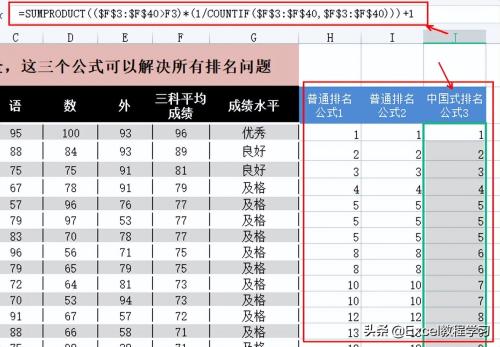
这个公式中嵌套了一个countif函数,通过公式2的介绍,我们知道了countif函数的表达式和作用,那么在这个公式中,它的条件为”$F$3:$F$40“,这是一个单元格区域。
以区域作为条件,则countif函数将从该区域中首个单元格开始,依次进行条件判断,即首先判断F3的值在计数区域中个数,在计算F4的值……一直到最后F40的值在计数区域中的个数,如果单元格的值在计数区域中有相同的,如F7的值77,在计数区域中还有两个单元格的值相同,那么countif函数公式的结果就是3.
这时作者在公式中”1/COUNTIF()“便表示1除以3,也就是1/3,而F8,F9的公式计算值也是1/3。
于是"1/COUNTIF()"的值再与"$F$3:$F$40>F3"相乘,$F$3:$F$40>F3是一个判断表达式,返回的结果为1或者0,其实与公式2中countif函数的条件作用相似。
两者相乘,再通过乘积求和函数sumproduct进行计算,它的执行结果如下图所示:
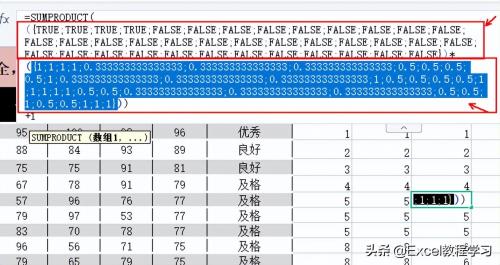
也许从这个截图中看不出它的含义所在,还需要多进行sumproduct函数的实操应用,多解析它公式各部分的结果值,来分解计算。
公式四:倒数排名RANK函数
第四个公式,又回到了作者讲的第一个公式rank函数,其实只要设置一下rank函数的第3参数排名方式,便可以达到倒数排名的效果。
如下图所示公式:=RANK(F3,$F$3:$F$40,1)
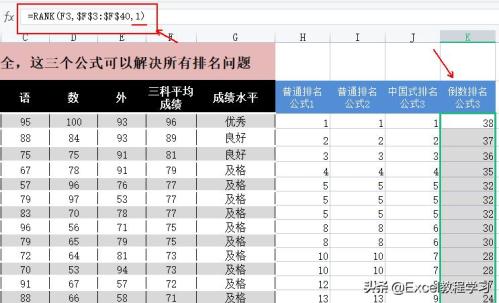
rank函数的排名方式只有两种,一个是0值的升序排名,另一个则是非0值的降序排名,这里我们设置参数为非零值1,执行降序排名,三科平均成绩最高的学生排名反而是最后一名,成绩最低的是第1名。









